La programación y la matemática son dos disciplinas que están estrechamente relacionadas, la matemática es la base fundamental de la programación, y su influencia se puede apreciar en cada línea de código que se escribe.
En este artículo, exploraremos cómo la matemática influye en la programación y cómo ambas se complementan entre sí este link muestra cada uno de los ejemplos que se ejecutan en el siguiente archivo de google Colab.
https://colab.research.google.com/drive/1AEXgja6BXCiPaIocMFEnxNlVbTli0g89?usp=sharing
1. Lógica y Algoritmos
La programación se basa en la lógica y los algoritmos, y la matemática proporciona las herramientas necesarias para desarrollar ambos. La lógica matemática es fundamental para resolver problemas de programación y tomar decisiones lógicas en el código. Los algoritmos, que son secuencias de instrucciones lógicas, también se basan en principios matemáticos.
Ejemplo práctico que involucra la determinación de si un número es primo mediante un algoritmo en un lenguaje de programación como Python:
def es_primo(numero):
# Verificar si el número es menor o igual a 1
if numero <= 1:
return False
# Iterar desde 2 hasta la raíz cuadrada del número
for i in range(2, int(numero**0.5) + 1):
# Verificar si el número es divisible por algún valor en el rango
if numero % i == 0:
return False
# Si no se encontraron divisores, el número es primo
return True
# Ejemplo de uso
numero_dado = 17
if es_primo(numero_dado):
print(f"{numero_dado} es un número primo.")
else:
print(f"{numero_dado} no es un número primo.")
17 es un número primo.
2. Estructuras de Datos
Las estructuras de datos son fundamentales en la programación, ya que permiten organizar y almacenar datos de manera eficiente. La matemática proporciona conceptos como conjuntos, listas, matrices y árboles, que son utilizados para representar y manipular datos en los programas. Además, los algoritmos matemáticos se utilizan para realizar operaciones en estas estructuras de datos.
En este ejemplo, la lista de Python se utiliza como una estructura de datos para almacenar números. La función sorted() aplica un concepto matemático, el ordenamiento, para organizar la lista en orden ascendente.
# Utilizando una lista como estructura de datos para almacenar elementos
mi_lista = [3, 7, 1, 4, 2, 8]
# Aplicando un concepto matemático (ordenamiento) para organizar la lista
mi_lista_ordenada = sorted(mi_lista)
# Imprimiendo la lista original y la lista ordenada
print("Lista Original:", mi_lista)
print("Lista Ordenada:", mi_lista_ordenada)
Lista Original: [3, 7, 1, 4, 2, 8]
Lista Ordenada: [1, 2, 3, 4, 7, 8]
3. Cálculo y Análisis Numérico
El cálculo y el análisis numérico son áreas de la matemática que son de gran importancia en la programación. Estas ramas de la matemática se utilizan para resolver problemas complejos que involucran cálculos y operaciones matemáticas avanzadas.
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
import numpy as np
# Definir la ecuación diferencial para simular el movimiento
def ecuacion_diferencial(t, y):
return [y[1], -y[0]]
# Configurar condiciones iniciales
condiciones_iniciales = [1, 0]
# Definir el intervalo de tiempo
tiempo_inicio = 0
tiempo_final = 10
intervalo_tiempo = (tiempo_inicio, tiempo_final)
# Resolver la ecuación diferencial utilizando scipy
solucion = solve_ivp(ecuacion_diferencial, intervalo_tiempo, condiciones_iniciales, t_eval=np.linspace(tiempo_inicio, tiempo_final, 100))
# Graficar la solución en el espacio tridimensional
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(solucion.y[0], solucion.y[1], solucion.t)
ax.set_xlabel('Eje X')
ax.set_ylabel('Eje Y')
ax.set_zlabel('Tiempo')
plt.show()
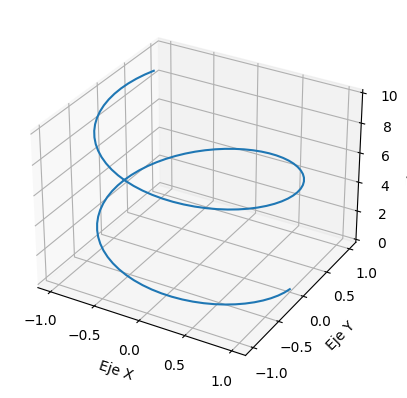
Por ejemplo, en la programación de gráficos 3D, se utilizan ecuaciones diferenciales para simular el movimiento y la interacción de objetos en un espacio tridimensional.
4. Criptografía y Seguridad
La criptografía es una rama de la matemática que se utiliza para garantizar la seguridad de la información en la programación. Los algoritmos criptográficos utilizan conceptos matemáticos como funciones hash, números primos y teoría de números para cifrar y descifrar datos. Sin la matemática, la seguridad de la información en el mundo digital sería prácticamente imposible.
import hashlib
# Función para crear un hash utilizando SHA-256
def crear_hash(texto):
hash_obj = hashlib.sha256(texto.encode())
return hash_obj.hexdigest()
# Ejemplo de uso
mensaje_original = "Informacion confidencial de Audra"
hash_resultante = crear_hash(mensaje_original)
# Imprimir el mensaje original y el hash resultante
print("Mensaje Original:", mensaje_original)
print("Hash Resultante:", hash_resultante)
Mensaje Original: «Informacion confidencial de Audra»
Hash Resultante: ‘4b5cc750137c08f8b89c8d8449ff6db469454cb324b3782cb88fef414d401e11’
5. Inteligencia Artificial y Aprendizaje Automático
La inteligencia artificial y el aprendizaje automático son campos de la programación que se basan en conceptos matemáticos como el álgebra lineal, la estadística y la probabilidad. Estos campos utilizan algoritmos matemáticos para analizar grandes cantidades de datos y tomar decisiones basadas en patrones y tendencias. La matemática es esencial para desarrollar modelos matemáticos que permitan a las máquinas aprender y mejorar su rendimiento con el tiempo.
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import numpy as np
# Generar datos de ejemplo
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# Dividir los datos en conjuntos de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Crear un modelo de regresión lineal
modelo = LinearRegression()
# Entrenar el modelo con los datos de entrenamiento
modelo.fit(X_train, y_train)
# Realizar predicciones en los datos de prueba
predicciones = modelo.predict(X_test)
# Graficar los resultados
plt.scatter(X_test, y_test, color='black')
plt.plot(X_test, predicciones, color='blue', linewidth=3)
plt.xlabel('Variable Independiente')
plt.ylabel('Variable Dependiente')
plt.title('Ejemplo de Regresión Lineal en Aprendizaje Automático')
plt.show()

Ejemplo simple utilizando Python y la biblioteca scikit-learn para entrenar un modelo de regresión lineal, que es un componente común en el aprendizaje automático:

La programación y la matemática son dos disciplinas que están estrechamente relacionadas, la matemática es la base fundamental de la programación, y su influencia se puede apreciar en cada línea de código que se escribe.






5 respuestas a “La Matemática y su impacto en la Programación”
Well written post! This is a really fantastic post, and we will link to it on our website. Continue your fantastic writing.
Thanks I have recently been looking for info about this subject for a while and yours is the greatest I have discovered so far However what in regards to the bottom line Are you certain in regards to the supply
Mat6tube This is my first visit here, and I’m so happy to read everything all in one spot
FlixHQ I like your website, although you should double-check the spelling on a few posts. Some of them are full of spelling errors, which I find bothersome, but I’ll definitely visit again.
Mitolyn I just like the helpful information you provide in your articles